|
Strange Ballistics |
||


|
Most WWII firing tables will conform in some way to a standard Gâvre drag function. Some however defy any comparison to a shell using one of the standard drag functions. This may be because of a non-standard shape or weight-cross-section. Or the testing laboratory didn't correctly determine the firing table of the shell. In any case I found several of these shells that some variable function had to be added into the drag equation to match firing table data. |
||
|
"All firing tables prepared by the Laboratory before 1943 depended on a limited number of standard drag functions and drag coefficients which had been worked out for generic types of projectiles between the wars. Whenever a drag function was needed for a projectile of new design, the function already established for the type of projectile most closely resembling the new design was used. By 1943, however, the use of solenoid chronographs in conjunction with electronic counters made possible the rapid and accurate calculation of drag functions for new projectiles on a fully experimental basis. When these data were used in the preparation of firing tables and these tables were compared with others based on the old standard drag functions, the advantages of the new procedure were clearly evident." |
||
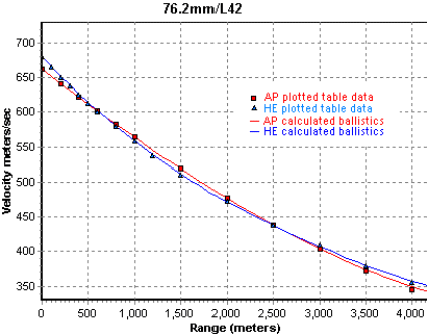
|
One of the strangest of all. The 76.2mm/L42 O-350 HE shell. This is shown in blue. The 76.2mm/L42 BR-350 APBC shell is shown in red. The HE shell first loses velocity very fast but somehow picks up speed around 2000 meters and gains the lead again at 3000 meters. |
||
|
With the improved accurate calculation of drag function since 1943 custom drag functions for each shell could be tailor-made. These would then need only a constant ballistic coefficient. In fact the ballistic coefficient would be 1.0 or not even be needed as the exact drag would be read from the drag function. Another function would not need modify the ballistic coefficient as a function. Since I don't have the kind of data to create a custom drag function and expertise I have to use another function to model the ballistics coefficient. The six standard Gâvre functions can be used for almost any shell as long as the ballistic coefficient varies in some degree with range to model these strange ballistic examples. So I have developed a a modifier to change the ballistic coefficient if needed. |
||
|
German 37mm/L45 AP is in red. Compare that to the HE shell in blue. |
||
|
US M3 75mm firing M61 AP is in green. Compare that to the M48 HE shell in black. |
||
|
The 88mm FlaK gun presents a more normal comparison. The heavier AP shell is in red while the lighter HE shell is represented by the blue line. |
||
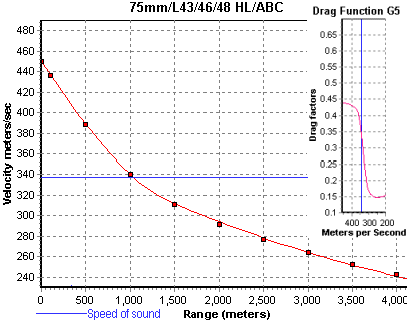
|
The 75mm HEAT shells HL/A, B and C have rather strange ballistics compared to other shells. This though is explained by the low muzzle velocity which makes the velocity level transcend the speed of sound. The drag resistance of the shell goes from high drag to a low drag level as it slows down passing through the (blue line) sound barrier (~337m/s) at around 1000 meters. |
||

