Post War Tank Gun Accuracy

Post war studies in tank gun accuracy become more detailed and various ballistic errors are broken out where dispersion is only one of them.  Errors in US and UK studies are now given in mils and in standard deviation.  Mils are equal to 1/6400 of a circle or  0.05625 degrees.   The first post war study I found is on a HEP (high explosive plastic) firing gun. The shell contains plastic explosive which when it detonates on steel armor the explosion scabs metal on the interior side which damages the inside of the tank.
1. 1956 TEST OF SHELL HEP, T170E3 FIR 76MM GUN T91[PDF]
1952 tests: probable error mils                                 1953 tests  probable error mils             
Accuracy  vert.=.35    hor=.33                                     Accuracy vert = .27  hor=.14
Converting to 50% zone in at 1000 yds:   tan(mils x 0.05625) x 1000 x 1.349 =
Accuracy  vert.= 0.464 yd    hor= 0.437 yd                 Accuracy vert = 0.358 yd  hor= 0.185 yd
HEP rounds are like HE and HEAT rounds and are not as accurate as AP type rounds.

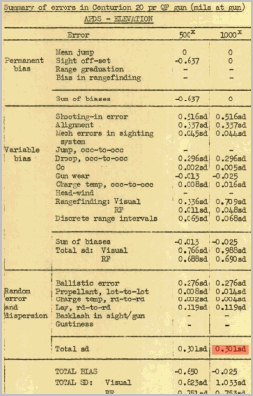
The next UK report really details the errors involved in accuracy.    One thing is to note how the total standard deviation are combined.  The square of the total equals the sum of the squares of the different components of error.  Or SD² = A² + B² + ... Z².

2. A. R. D. E. Report (B)/58 [PDF] Classification of errors involved in the determination of chance of hit with Centurion under quasi battle conditions. 1958
Two rounds are reported on from the 20-pdr; APDS and HESH (HESH is the British name for HEP) round.
First round hit chance of a 7.5 foot square target at 1000 yd.
71.8% APDS      25% HESH
There are quite a number of error factors given though I am only including the s.d. of the dispersion.
APDS elevation: dispersion=0.301sd; 50% zone= 0.301 x 1.349=0.399 yd
           line: dispersion =0.288sd         50% zone = 0.288 x 1.349 = 0.381 yd.
HESH elevation: dispersion=0.32       50% zone= 0.32 x 1.349=0.423 yd
            line:  dispersion=0.455            50% zone= 0.455 x 1.349=0.60 yd

While all the different reasons for in-accuracy are interesting other than shell dispersion including gun jump they could all be lumped into what might be called shooting error. 

3. A 1959 US study THE EFFECT OF SYSTEM DESIGN CHARACTERISTICSON FIRST ROUND HITTING PROBABILITY OF TANK FIRED PROJECTILES (U [PDF] looks like it takes a lot of the theory from the previous British report.  In this an abstract projectile has a horizontal 0.3 mil sd dispersion and a 0.25 mil sd jump error. And a vertical 0.3 mil sd dispersion and 0.31 mil sd jump error.  As well as a similar 7.5' square target.   From a graph it looks like the M1A2 M79 round in 'quasi' battle conditions would have around a 30% chance of a first round hit at 1000yds. The M62 round from the same gun is about 38% under the same conditions but the graph is blurry.
Looking at dispersion alone we have 0.3 mil = 0.295 x 1.349 = 0.397 yd horizontal and vertical.  If we were to include the jump and dispersion then for horizontal we would get : .431 > 0.424 x 1.349= 0.572 yd; .3905 >.383 x 1.349=0.517 yd.  In any case considerably more than the h= 0.277 v= 0.225 as reported in item #2 on page 38.
I'm not sure whether jump or any variable error should be part of dispersion or as range error.

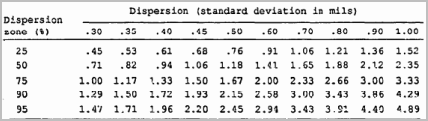
4. Looking at the 1988 Projectile Dispersion of the 25mm Cannon on the Bradley [PDF] a table (shown at right) is given comparing 50% zone and 90% zone.  This 90% zone stated in mils averages ~1.825 x the 50% zone.  And the 50% zone is about 2.35 times the standard deviation in

mils.
The report gives a formula (1. to the right) for finding the diameter of the dispersion zone in terms of sd.  In the formulas to the right C is the Chi-Square 2 degrees of freedom. In formula 2. D is the diameter of a circle with the std dev where the x and y dispersion is the same. To find the Chi-square Distribution we have to search for the table on the net.  For .5 =1.39 and .9=4.61.   Finding the square root then multiplying by 2 x .3 we get: 50% = .707 s.d and 90%=1.288.  What if we want

to convert 90% zone to a 50% German zone?  Tan(1/4.29 x s.d.) x 1000 x 5.488 =  5.488 x size.
Another test would be to show the 0.3 mil s.d. vs. a 1m x 2m target. 0.3 mil = tan(0.3 x 0.5625) x 1000 x 1.349 = 0.397m 50% dispersion zone.  By the Ballistic Accuracy calculator this would produce a 91% chance at 1000m which is exactly what table 3 shows.  Or for a 4' x 4' target a 93% chance to hit a 1000m.  This verifies that when converted from mils to meters of s.d. and run through the German style dispersion hit formula the results are the same.
The 50% radius is the circular probable error, generally referred to as CEP value is found to be 1.1774.

5. Ammunition 76mm and 90mm for Scorpion tank [PDF]
76mm HESH, HE                                             1.22 mils  50% zone =  1.62 m.
90mm APFSDS  1200 m/s dispersion less than .3 mils,   50% zone = 0.398 m at 1000 m.

6. Hit Probabilities of a High Velocity Tank Round [PDF]1993
APFSDS 1600 m/s 4000m 1345m/s v=.25 h=.26 mils.   v=0.33 m  h=0.34 m.

7. The Tank Accuracy Model [PDF]1993  US 120mm
From table: Pure ballistic dispersion  v=h= 0.21 mils This would be a 50% zone of 0.278 m @ 1000m  But the random error includes the targeting system error found in the code which is v=h=0.197 mils.  Together using the sum of the squares method results:  0.29 mils.  Giving a 50% zone of  0.384 m @ 1000 m.

8. Russian 125mm gun  mean deviation h=0.27m v=0.27m  50% zone:  0.456 m @ 1000 m
BM 12                          mean deviation h=0.27m v=0.27m
APFSDS rounds (0,2mil dispersion for HEAT-FS and 0.25-0.3 mils for APFSDS: 0.353 m @ 1000m)
Note - Russian mils are larger than US mils.  They are .06 degree or 360/6000 of a circle.
9. Russian maximum dispersion = .25 mils.  50% zone: 0.353 m @ 1000m

10. Zeroing In [PDF]1995
M829
APFSDS-T
0.5 mils total error h and v.    50% zone: 0.662 m @ 1000m

11. Polish Ammunition for 120mm  [PDF]   in Russian mils.
APFSDS=.2 mils   50% zone: 0.283 m @ 1000m   HE=.3 mils

12. Pakistan Ammunition defense  125mm in Russian mils.
APFSDS v=h=0.23-.25      50% zone:  0.325- 0.353 m @ 1000m
HEAT     v=h=0.21    0.297 m.

The conclusion is that the random shot to shot error can be separated into shell dispersion and jump error. Trying to work backwards from WWII live fire hit percentages to find shell dispersion like I tried on item # 5 page 40 may be a fool's errand.