American Tank Gun Accuracy

You would think that determining the gun accuracy of US guns would be easy.   Finding data is pretty easy but what is found conflicts with other data.  The first gun we will look at is the ubiquitous 75mm M2 and M3 guns.   
1. The dispersion of the M3 was found by tests at Aberdeen as well as the University of New Mexico. The mean dispersion is hor.=0.347 yd,  vert.= 0.246 yd @ 1000 yds for University of New Mexico and hor= 0.349 yd and vert= 0.374 yd at 1000 yd for Aberdeen. Averaging gives hor.= 0.348 yd and vert.= 0.31 yd. This comes out of the Sabot Tests of 1942-1944.

2. Another data point is found post war with the Tank Fire control systems (1955). 75mm M3 from M4A2 tank standard deviation mils at 500 yds. To go from US s.d. to German type 50% zone dispersion multiply by 1.349.
The problem you cannot just double the deviation at 1000 yds.  Deviation would grow at 1000 yds for example the Russians measured the deviation of the 3" M7 gun at 500 m and 1000m.  Link
Stationary Fire:  h= 0.21 v=0.17 in mils @500yds =0.206  v=.167;  multiply  by 1.349; h= 0.277 v= 0.225.
"Capacities and Limitations of Moving Fire with Gyrostabilizer," Armored Medical Research Laboratory,
Fort Knox, Kentucky, 24 May 1944, RESTRICTED, (Ref. 2).
Deviation grows from 500 to 1000 by a factor of  (X=2.4, Y=2.33) .  Result (0.676, 0.524 )  This is just an estimate.
3. Weapon Research Committee: accuracy of anti-tank guns and rigidity of gun barrels", 1948 [PRO piece number WO 195/10134],
Gun  Ammunition m.v. (f.p.s.)  Ave m.d. (mean deviation) of strike     
75mm M3            APC  2030       0.5 minutes.   :    Tangent (0.5/60) x 1000 x  1.69 =
That equates to a 50% zone = 0.246 yd @ 1000 yds
(To be real accurate first divide the angle by 2, then find the tangent then multiply the results by 2 at the end.)

4. British AORG Memo No. 514:

Pure ballistic mean deviation of strike is given, without range error:
75mm  M3        APCBC:    0.9 minutes 
The mean average strike of 0.9'= tangent( 0.9/60) x 1000=  0.261 yd. x 1.69 = 0.442 yd

5. M2 gun  M61 M72 rounds
Russian data on American guns is seen to the right. 75 mm M2, from the M3 Lee.
This is probable error of APCBC shell M61 and AP shot M72:
Vertical: 30 cm
Horizontal: 30 cm
(Russian  probable error is deviation 1/2 of the 50% zone.)
That calculates out to a 50% zone of v=0.60m  h=0.60m at 1000m. Which would also be v=0.6 yd and h=0.6 yd at 1000 yds.

6. The dispersion table shown to the right is from a Russian table on the 75mm M2 gun firing the M48 round.  The mean vertical dispersion at 1000m is 0.4 meters. This converts to a vertical 50% zone of 0.4 x 2 = 0.8 yd.

7. The image on the right is from a British War Office document of the 75mm M3 firing the M48 round where the vertical 90% dispersion zone at 1000 yds is 3 feet from center. The 90% zone dimensions would normally be 2.44 times the 50% zone, however British and US dispersion distance from the point of aim or 0.41 yds. 
Some more British tests.  A bit of transition to the British version of the

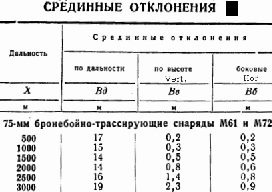
M3 75mm gun which is the Q.F. 75mm Mk V.  This fired the M72 round as well as the M61 with an inert filler.
8. WO 291/238 AORG Report No.256 "The Importance of Gun Dispersion in A.P. Shooting" provides data comparing accuracy/dispersion of tank mounted guns. This gives the following data for a number of tank guns at 1000 yards range. (presumed to be 90% zone)  To find the German 50% zone from UK 90% zone divide by 2.44,
Gun                                   dispersion
75mm M3 APCBC (M61)   2.2 mins     Tangent (2.2/60) x 1000/2.44 = 0.262 yd.         
75mm Mk.V APCBC          3.0 mins     Tangent (3/60) x 1000/2.44    = 0.358 yd.         
76mm  APCBC                   1.4 mins     Tangent (1.4/60) x 1000 /2.44 = 0.167 yd         
* Alternately using the BA program to find dispersion that results in 90% hit chance of dispersion sized target.

76mm M1A1 and 90mm M3

9. Weapon Research Committee: accuracy of anti-tank guns and rigidity of gun barrels", 1948 [PRO piece number WO 195/10134],
Gun  Ammunition m.v. (f.p.s.)  Ave m.d. (mean deviation) of strike     
76mm   M1A1 APCBC    2600           0.5'              : tangent (0.5/60) x 1000 x 1.69  = 0.246 yd.
                          AP/T      3400           0.5'              : tangent (0.5/60) x 1000 x 1.69  = 0.246 yd.
90mm   M3     APC          2600           0.3'              : tangent (0.3/60) x 1000 x 1.69  = 0.147 yd.
                       AP/T         3350           0.5'              : tangent (0.5/60) x 1000 x 1.69  = 0.246 yd.

10. Armor -Piercing Ammunition for Gun, 90-mm, M3
M82:      APCBC   2800 f/s extreme horizontal dispersion 41 in., vertical 70 in. at 2100yds.
T-33:       AP          2800 f/s extreme horizontal dispersion 16 in., vertical 19 in. at 700yds.
T30E15: HVAP     3400 f/s extreme horizontal dispersion 17 in., vertical 30 in at 2100 yds.
M82:  41/36  x 1000/2100 = 0.542 yd,  70/36 x 1000/2100= 0.956 yd;   T-33: 16/36 x 1000/700 =0.635 yd, 19/36 x 1000/700 = 0.754 yd.
T30E15: 17/36 x 1000/2100 =0.225 yd,   30/36 x 1000/2100 =.0397 yd.

The question now becomes what do they mean by extreme?  Is that the 90%, 95% or 99.7% zone?  So we might as well figure out the numbers in all cases.   90% zone = 2.44 x 50% zone, 95% zone =2.91 x, and 99.73% is 3 x.
Since this is a US zone I assume it must be divided by 2 to conform to German/Russian standards.
  [90%,95%,99.7%] Giving:
M82: h=[0.444, 0.373, 0.381] v=[0.784, 0.657 , 0.637]
T-33: h=[0.52, 0.436 , 0.423] v=[0.616, 0.518 , 0.503]
T30E15: h=[0.184, 0.155, 0.15] v=[0.325, 0.273, 0.265]

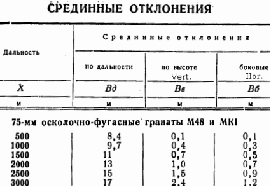
The results are somewhat confounding.  The US/UK 75mm guns sometimes have small dispersion, sometimes large.  It might be attributed to differing quality lots of ammo or maybe something else for the unusually small dispersions.  One reason may be the way probable statistics are defined.  At least in regard to US/UK definitions of percent zones as compared to German/Russian definitions.     
11. According to note no. 4 found in  3-1-1951 FOREIGN FIRING TABLES for SOVIET GUN, Self-