Ballistic Accuracy Computer

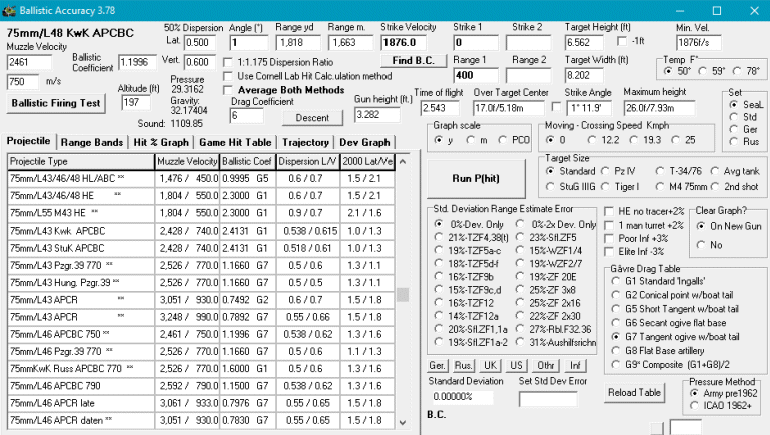
1. The Ballistic Accuracy program is what I use to calculate the to hit values.  These are the theoretical probabilities of obtaining a hit with a projectile aiming at dead center the target area.  For many years this has been based in part on the corrected formula in the book World War II Ballistics Armor and Gunnery  (PDF) by Lorrin Bird and Robert Livingston.
I recently found a report from 1969 of a Probability to hit formula by Cornell Aeronautical Laboratory[PDF] done for the Naval Research department at Dalhgren, VA.  While both formulas go at solving the problem in different ways both solutions converge at longer ranges.   So lets take a look at the program menu.

2. The main menu is divided into two main functions.  The upper regions involve the ballistics of firing of a single projectile. This is for testing the various ballistic factors of a round.  Below this the function is to determine the probable hit percentage at a target under selected circumstances.  This calculates the probability to hit at many ranges and

takes a few seconds to run.
3. The program uses the ballistics formula by Robert McCoy. Found in his book Modern Exterior Ballistics. As such it can select the firing elevation and temperature.
I originally used the K ballistic drag factors supplied by Bird and Livingston then converted to ballistic coefficient (BC) as my ballistic coefficient but they proved inaccurate for the program.  Now the program can calculate its own drag as long as it has the velocity at two points in the trajectory.    (Sometimes ballistic coefficients can change with range.)
4. Left is an example of a comparison of the two formulas.  The gun is the 88mm of the Tiger Ausf E tank firing a first shot APCBC round at a T-34/76 sized target with an 16% standard deviation ranging error. 

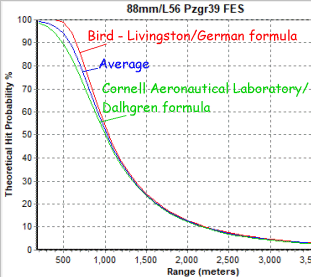
As you can see both formulas produce a probability curve that remarkably converge to a single line around 1000m.  I'm not sure why it diverges at shorter ranges but that is why I take an average. I haven't converted my tables to the new formula but stay tuned.

5. The original Bird-Livingston formula had an error in it.  It doubled the dispersion.  I only found this out when I set the ranging error to zero and tried to mimic the German accuracy tables.  When this problem is corrected the German Dispersion and Firing tables can be recreated to a high degree.   Below to the left a copy of the German firing table for the 88mm/L71 shows the Accuracy with just dispersion (left most column) and firing (2 x dispersion) is nearly identical to the results from the Ballistics program when ranging error is set to zero.
Illustration of trajectory on target. 

other hit graphs: 88mm/L71   122mm D-25T  17pdr  76mm M1A1 F-34  75mm/L48  85mm/L53
   Garve Functions G1, G8, G9
How to use the Tafel der Wahrscheinlichkeitsfaktoren  (Table of Probability Factors).
Divide 2.5 by the lateral deviation.   Find that number on the first column of the  table and get the lateral percentage.
Divide 2 by the vertical  deviation.   Find that number on the first column of the  table and get the vertical percentage.
Multiply the vertical deviation percentage by the lateral deviation percentage to get the total dispersion percentage.
To find the German accuracy percentage double the dispersion values in the above calculations.
Tafel der Wahrscheinlichkeitsfaktoren

Note -the German table has a typo for the terminal velocity at 1900m

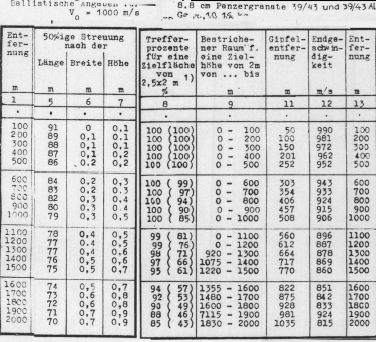
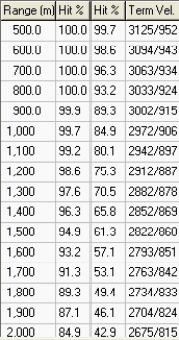
6 One way to manually compute the German dispersion and accuracy numbers for a target size of 2.50m x 2.0m. use the following formula:
Converting the 50% zone dispersion to terms of standard deviation.  Looking up the German values for 50% dispersion zones rounded to the nearest tenth at say 1500m we find:  lateral zone = 0.5m and vertical zone = 0.7m.   Divide each by 0.67449 to convert to standard deviations. (See Rheinmetall conversions.)

Lateral : 0.5m/0.67449 = 0.7413m               
vertical: 0.7m/0.67449 = 1.0378m
Compare target size to standard deviation (s.d.) to get a ratio of how much of the target is covered:
Lateral: 2.5m/0.7413m = 3.372 standard deviations.  This contains 99.91% lateral probability.
Vertical: 2.0m/1.0378m = 1.927 standard deviations.  This contains 94.6% vertical probability.
Multiply these together to get the total percentage to hit.
99.91% x 94.6% = 94.51% ~ 95% as listed at 1500m in the 88mm/L71 firing table.

Knowing this relationship to the German dispersion and accuracy numbers the 50% dispersion zone value can be found.  This may not be the only solution as the horizontal to vertical ratio can't be determined.   For now let's say it is 1 to 1. 
An example - I don't have the 50% zone of the German 37mm gun, but I do have the dispersion and accuracy values.
(Accuracy for the Germans is 2 x dispersion.)  Dispersion 90%@1000 and 47%@1500m.  Accuracy 47%@1000m and 15%@1500m.   Plugging in values for dispersion yields at 1000m=0.76m and 1500m=1.96m.  That is 1000m = 0.76m x 0.76m; 1500m = 1.96m x 1.96m.
At 500m the dispersion looks to be 0.43m x 0.43m.